The Sum Of Interior Angles Of A Triangle: A Comprehensive Guide

Lenny Ernser 20 Jun 2025

Understanding the sum of interior angles of a triangle is fundamental in geometry and mathematics as a whole. This concept is not only essential for students but also widely applicable in various fields such as architecture, engineering, and design. In this article, we will delve deeply into the principles, calculations, and applications of the sum of interior angles of a triangle.

Triangles are one of the most basic shapes in geometry, yet their properties hold profound significance in mathematical theories and real-world applications. By exploring the sum of interior angles, we can better understand the geometric principles that govern these shapes.

Whether you're a student preparing for an exam, a professional looking to apply geometric principles in your work, or simply someone curious about the intricacies of triangles, this article will provide you with all the information you need. Let's embark on this journey of discovery together.

Introduction to the Sum of Interior Angles of a Triangle
Basic Concept of Triangle Angles
Formula for Calculating the Sum of Interior Angles
Proof of the Sum of Interior Angles
Types of Triangles and Their Angles
Applications of the Sum of Interior Angles
Common Mistakes to Avoid
Real-World Examples
Tips for Solving Triangle Angle Problems
Conclusion

Introduction to the Sum of Interior Angles of a Triangle

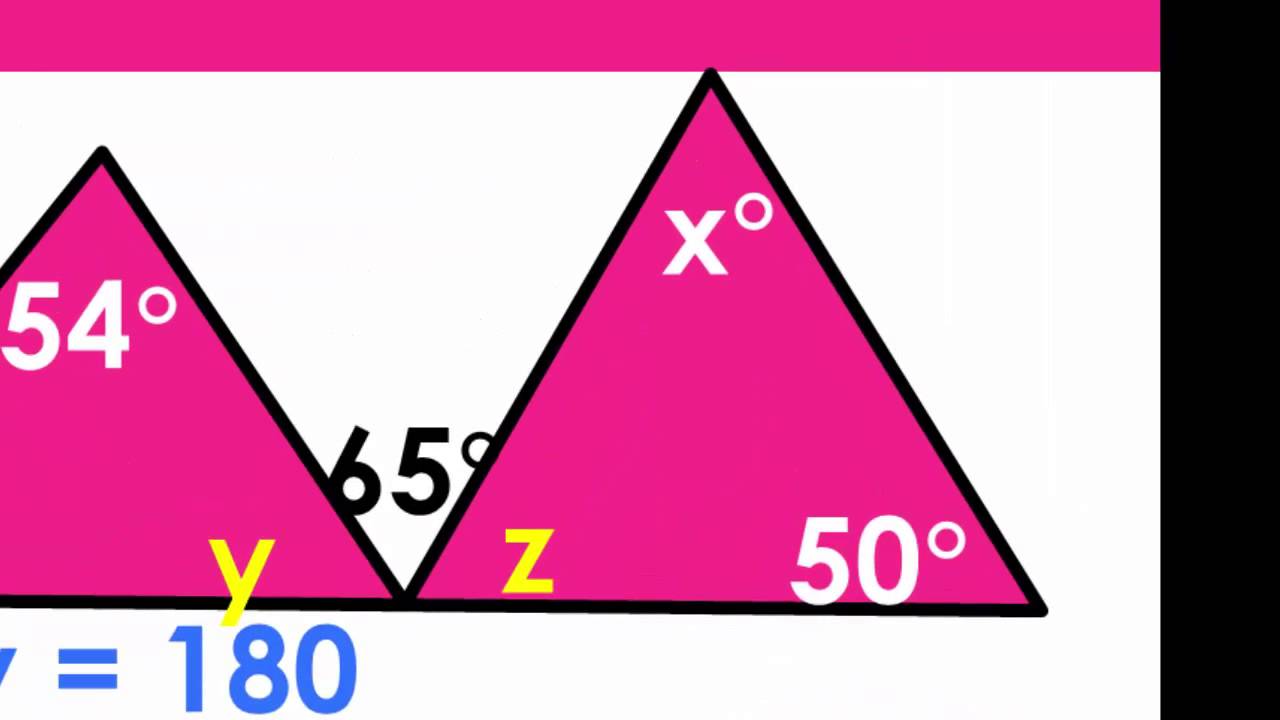
The sum of interior angles of a triangle is a foundational concept in geometry. This principle states that the sum of the three interior angles of any triangle is always 180 degrees. This rule applies to all types of triangles, regardless of their size or shape.

This concept is not only crucial for solving mathematical problems but also plays a significant role in various practical applications. Understanding this principle helps in fields such as architecture, where precise measurements are essential for designing stable structures.

In this section, we will explore why this rule holds true and how it can be applied in different scenarios. By the end of this discussion, you will have a clear understanding of the importance of the sum of interior angles in geometry.

Basic Concept of Triangle Angles

A triangle consists of three sides and three angles. The angles inside the triangle are known as interior angles. The sum of these three interior angles is always 180 degrees, which is a fundamental property of triangles.

Understanding the Properties of Triangles

Triangles have three sides and three angles.
The sum of all interior angles equals 180 degrees.
This property is consistent across all types of triangles, including equilateral, isosceles, and scalene triangles.

This basic concept forms the foundation for more complex geometric theories and calculations. By understanding the properties of triangles, we can solve a wide range of mathematical problems.

Formula for Calculating the Sum of Interior Angles

The formula for calculating the sum of interior angles of a triangle is straightforward. It can be expressed as:

Sum of interior angles = 180 degrees

Applying the Formula

Let’s consider an example:

Suppose you know two angles of a triangle: 50 degrees and 60 degrees.
To find the third angle, subtract the sum of the two known angles from 180 degrees.
Third angle = 180 - (50 + 60) = 70 degrees.

This method is simple yet effective for solving problems related to triangle angles.

Proof of the Sum of Interior Angles

The proof for the sum of interior angles of a triangle is based on the principles of parallel lines and transversals. By drawing a line parallel to one side of the triangle through the opposite vertex, we can demonstrate that the sum of the angles is indeed 180 degrees.

Step-by-Step Proof

Draw a triangle ABC.
Draw a line parallel to side BC through point A.
Label the angles formed by the transversal as alternate interior angles.
Since the angles on a straight line sum to 180 degrees, the sum of the interior angles of the triangle is also 180 degrees.

This geometric proof provides a solid foundation for understanding the concept.

Types of Triangles and Their Angles

Triangles can be classified based on their angles and sides. The classification affects the properties of their angles. Here are the main types:

Equilateral Triangle

An equilateral triangle has all three sides and angles equal. Each angle measures 60 degrees.

Isosceles Triangle

An isosceles triangle has two equal sides and two equal angles. The third angle is different.

Scalene Triangle

A scalene triangle has no equal sides or angles. Each angle is unique.

Understanding these classifications helps in solving problems related to triangle angles.

Applications of the Sum of Interior Angles

The concept of the sum of interior angles of a triangle has numerous applications in real life. Here are a few examples:

Architecture and Engineering

Architects and engineers use this principle to ensure the stability and symmetry of structures. Triangles are often used in construction because of their inherent strength.

Navigation and Mapping

In navigation, the sum of angles is used to calculate distances and directions. Triangles are used to determine positions on maps and charts.

Computer Graphics

In computer graphics, triangles are the building blocks for rendering 3D models. The properties of triangles, including their angles, are crucial for creating realistic visuals.

These applications highlight the practical importance of understanding triangle angles.

Common Mistakes to Avoid

When working with triangle angles, it's easy to make mistakes. Here are some common errors to watch out for:

Incorrect Angle Measurements

Ensure that all angle measurements are accurate. A small error can lead to incorrect results.

Forgetting the Sum Rule

Always remember that the sum of interior angles is 180 degrees. This rule applies to all triangles.

Confusing Triangle Types

Be careful when classifying triangles. Misclassification can lead to incorrect angle calculations.

By being aware of these common pitfalls, you can avoid mistakes and improve your problem-solving skills.

Real-World Examples

Let’s explore some real-world examples where the sum of interior angles of a triangle is applied:

Building Construction

Architects use triangles to design roofs and trusses. The sum of angles ensures that the structure is stable and balanced.

Surveying

Surveyors use triangles to measure land and calculate distances. The sum of angles helps in creating accurate maps.

Art and Design

Artists use triangles to create balanced compositions. Understanding angles helps in achieving visual harmony.

These examples demonstrate the versatility and practicality of triangle angle principles.

Tips for Solving Triangle Angle Problems

Here are some tips to help you solve problems related to triangle angles:

Always start by identifying the type of triangle.
Use the sum of angles rule as a reference point.
Double-check your calculations to avoid errors.
Practice regularly to improve your skills.

By following these tips, you can enhance your ability to solve triangle angle problems effectively.

Conclusion

In conclusion, the sum of interior angles of a triangle is a fundamental concept in geometry. This principle applies to all types of triangles and has numerous applications in various fields. By understanding the properties of triangles and their angles, we can solve a wide range of mathematical problems and apply this knowledge in real-world scenarios.

We invite you to share your thoughts and questions in the comments section below. Feel free to explore other articles on our site for more insights into mathematics and geometry. Together, let’s continue to expand our knowledge and appreciation of the fascinating world of triangles.

For further reading, consider these trusted sources:

Interior Exterior Angles Triangle Worksheet Matttroy

Interior Exterior Angles Triangle Matttroy

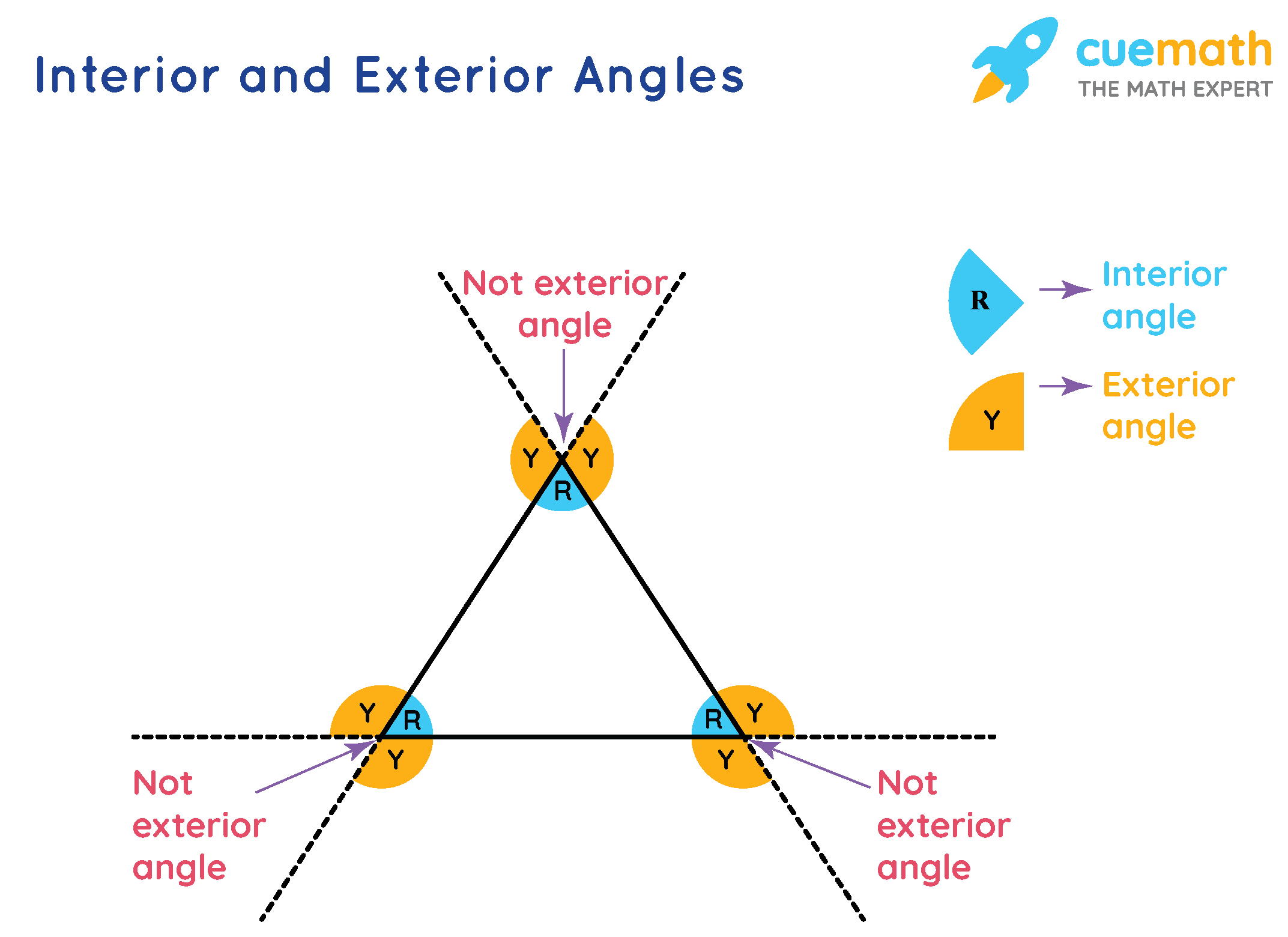
Interior Angles Of A Triangle Worksheet

True Celebs