The Sum Of Interior Angles Of A Triangle: A Comprehensive Guide

Christelle Streich 22 Jun 2025

Understanding the sum of interior angles of a triangle is fundamental in mathematics and geometry. Whether you're a student, educator, or simply someone curious about the basics of geometry, this article will provide a detailed explanation of the concept. From its mathematical foundation to its practical applications, we'll explore everything you need to know about the sum of interior angles of a triangle.

Triangles are one of the most basic yet essential shapes in geometry. They appear in various fields, including architecture, engineering, and design, making it crucial to understand their properties. Among these properties, the sum of interior angles stands out as a cornerstone of geometric principles.

In this article, we will delve into the mathematical reasoning behind the sum of interior angles of a triangle, its real-world applications, and how it connects to broader geometric concepts. By the end of this guide, you'll have a comprehensive understanding of this fundamental topic.

Introduction to Triangles and Their Angles
Mathematical Proof of the Sum of Interior Angles
Types of Triangles and Their Interior Angles
Real-World Applications of the Sum of Interior Angles
Common Misconceptions About Triangle Angles
Advanced Concepts Related to Triangle Angles
History of Triangles in Mathematics
Practical Examples of Calculating Triangle Angles
Frequently Asked Questions About Triangle Angles
Conclusion and Next Steps

Introduction to Triangles and Their Angles

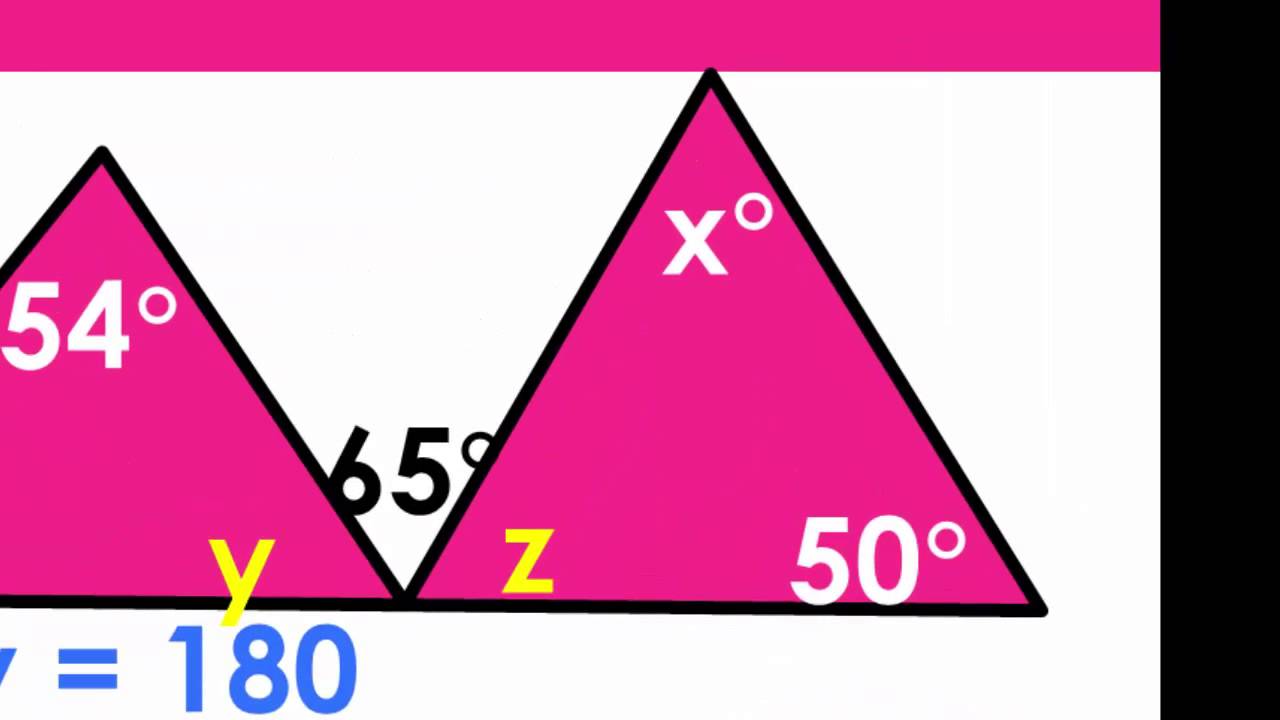
Triangles are three-sided polygons that form the foundation of Euclidean geometry. Every triangle has three interior angles, and the sum of these angles is always 180 degrees. This property holds true regardless of the type of triangle, whether it's equilateral, isosceles, or scalene.

The concept of the sum of interior angles of a triangle is not only a theoretical principle but also has practical implications. It allows mathematicians and engineers to solve complex problems involving shapes and structures. Understanding this concept is crucial for anyone studying geometry or working in related fields.

Why is the Sum Always 180 Degrees?

The sum of interior angles of a triangle is always 180 degrees due to the flat nature of Euclidean geometry. This principle is derived from the parallel postulate, which states that parallel lines never intersect. By dividing a triangle into smaller components, we can prove this property mathematically.

Mathematical Proof of the Sum of Interior Angles

To understand why the sum of interior angles of a triangle equals 180 degrees, we can use a simple geometric proof. Imagine extending one side of the triangle and drawing a line parallel to the opposite side. Using the properties of alternate interior angles and supplementary angles, we can demonstrate that the sum of the angles in a triangle is always 180 degrees.

Step-by-Step Proof

Draw a triangle and label its angles as A, B, and C.
Extend one side of the triangle and draw a line parallel to the opposite side.
Identify the alternate interior angles formed by the parallel line and the triangle's sides.
Sum the angles using the properties of parallel lines and supplementary angles.

Types of Triangles and Their Interior Angles

Triangles can be classified based on their sides and angles. Each type of triangle has unique properties related to its interior angles:

Equilateral Triangle

An equilateral triangle has three equal sides and three equal angles, each measuring 60 degrees. This symmetry makes it a special case in geometry.

Isosceles Triangle

An isosceles triangle has two equal sides and two equal angles. The third angle, known as the base angle, can vary depending on the triangle's dimensions.

Scalene Triangle

A scalene triangle has no equal sides or angles. However, the sum of its interior angles remains 180 degrees, as with all triangles.

Real-World Applications of the Sum of Interior Angles

The sum of interior angles of a triangle is not just a theoretical concept; it has numerous practical applications:

Architecture: Architects use triangle properties to design stable structures, ensuring that angles and dimensions align correctly.
Engineering: Engineers apply triangle geometry in designing bridges, buildings, and other infrastructure.
Navigation: Triangles are used in navigation to calculate distances and angles, especially in GPS systems.

Common Misconceptions About Triangle Angles

Despite its simplicity, the concept of the sum of interior angles of a triangle can lead to misconceptions:

Non-Euclidean Geometry: In non-Euclidean geometry, the sum of interior angles may not equal 180 degrees, depending on the surface curvature.
Curved Surfaces: On curved surfaces, such as spheres, the sum of angles can exceed 180 degrees.

Advanced Concepts Related to Triangle Angles

For those interested in deeper mathematical exploration, several advanced concepts relate to triangle angles:

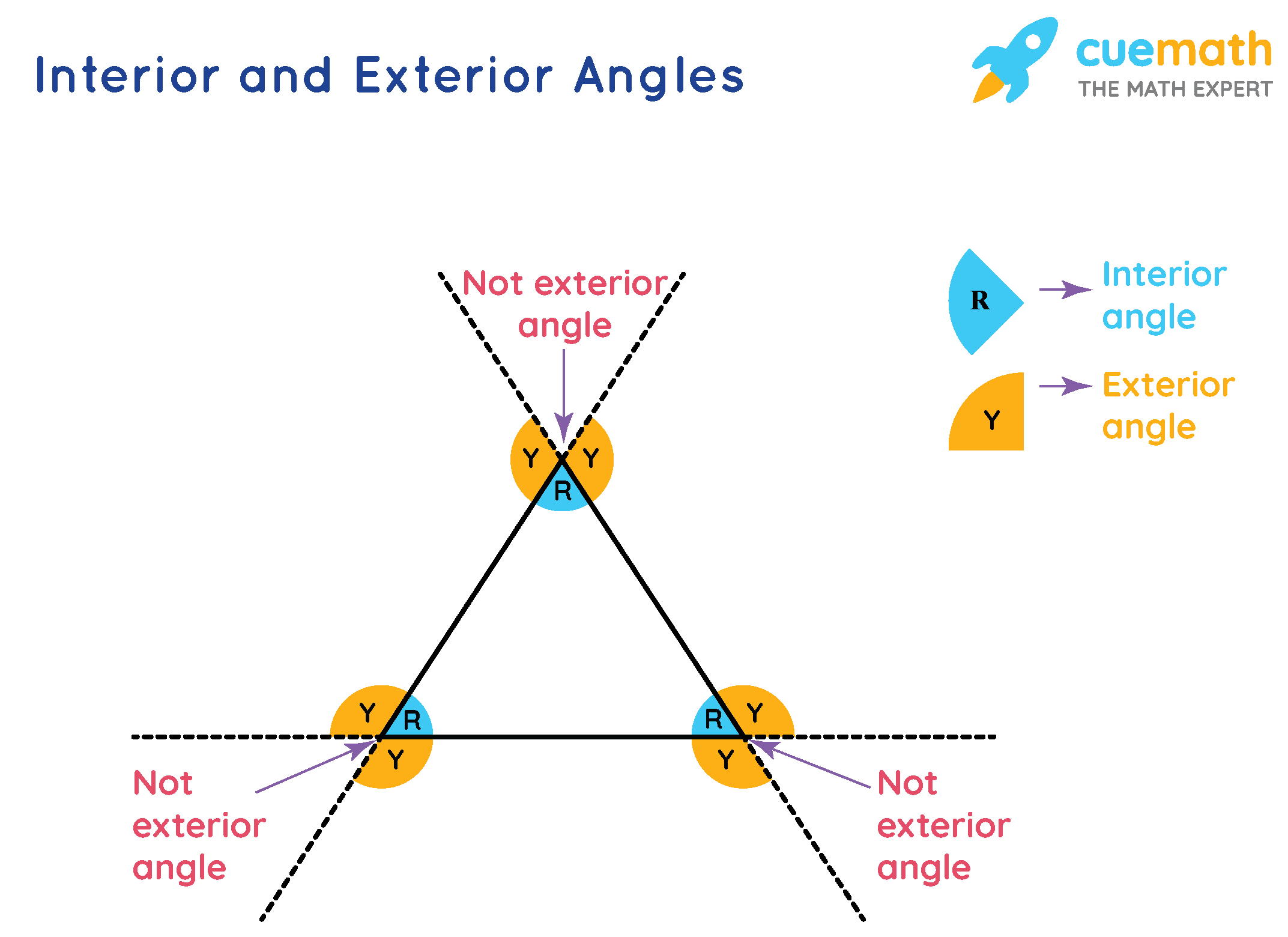
Exterior Angles

The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. This property is useful in solving complex geometric problems.

Trigonometry

Trigonometry extends the study of triangle angles by introducing sine, cosine, and tangent functions. These functions allow for precise calculations involving angles and sides.

History of Triangles in Mathematics

The study of triangles dates back thousands of years. Ancient civilizations, such as the Egyptians and Babylonians, used triangles in construction and astronomy. Euclid's "Elements," written around 300 BCE, formalized many geometric principles, including the sum of interior angles of a triangle.

Practical Examples of Calculating Triangle Angles

Here are some practical examples to help you apply the concept of the sum of interior angles:

Example 1: Solving for Missing Angles

If two angles of a triangle measure 50 degrees and 60 degrees, what is the third angle?

Solution: Subtract the sum of the two known angles from 180 degrees.

180 - (50 + 60) = 70 degrees

Example 2: Using Trigonometry

If one side of a triangle measures 10 units and the opposite angle is 30 degrees, use trigonometric functions to find the other sides and angles.

Frequently Asked Questions About Triangle Angles

Q: Can the sum of interior angles of a triangle ever exceed 180 degrees?

A: In Euclidean geometry, the sum of interior angles of a triangle is always 180 degrees. However, in non-Euclidean geometry, such as on a sphere, the sum can exceed 180 degrees.

Q: How are triangles used in real life?

A: Triangles are used in architecture, engineering, navigation, and various other fields to ensure stability and accuracy in designs and calculations.

Conclusion and Next Steps

In conclusion, the sum of interior angles of a triangle is a fundamental concept in geometry with wide-ranging applications. Whether you're solving mathematical problems or designing real-world structures, understanding this principle is essential. We encourage you to explore further by studying advanced topics like trigonometry and non-Euclidean geometry.

Feel free to leave a comment or question below. Share this article with others who might find it helpful, and don't forget to explore our other geometry-related content for more insights!

Interior Exterior Angles Triangle Worksheet Matttroy

Interior Exterior Angles Triangle Matttroy

Interior Angles Of A Triangle Worksheet

True Celebs